国债期货价格的计算并非简单的算术运算，而是基于一系列复杂的理论变量和模型。准确预测国债期货价格，需要深刻理解这些变量之间的互动关系以及它们如何受到市场环境变化的影响。将深入探讨计算国债期货价格所用到的关键理论变量，并对这些变量的特性进行详细分析。

1. 现券收益率曲线

现券收益率曲线是计算国债期货价格最重要的基础变量之一。它反映了不同期限国债的收益率水平，通常以图形的形式表示，横坐标为债券期限，纵坐标为收益率。收益率曲线并非平滑的直线，其形状会随着市场预期和经济环境的变化而波动。例如，正常情况下，收益率曲线向上倾斜，表示长期债券收益率高于短期债券收益率，这体现了投资者对长期投资的风险溢价要求。在经济衰退预期或货币政策宽松时期，收益率曲线可能出现倒挂（短期收益率高于长期收益率），这通常被视为经济衰退的预警信号。计算国债期货价格时，需要选择与期货合约标的债券期限相匹配的现券收益率，并以此作为估值的基础。不同的插值方法（例如线性插值、多项式插值等）会对最终计算结果产生一定的影响。收益率曲线的形状和斜率也蕴含着市场对未来利率走势的预期，这会直接影响到国债期货的定价。

2. 期货合约的交割月份和标的债券

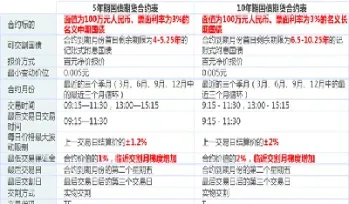
国债期货合约的交割月份和标的债券是决定期货价格的重要因素。不同的月份合约反映了市场对未来不同时期利率的预期，因此价格也会有所差异。例如，在预期利率上升的环境下，远期合约的价格通常会低于近月合约的价格（期货价格曲线向上倾斜）。而标的债券的具体属性，例如久期、票息率等，都会影响期货合约的价值。期货合约通常会指定一个或多个可交割债券，投资者可以选择其中一种债券进行交割。在计算期货价格时，需要考虑所有可交割债券的收益率和价格，并根据其权重进行加权平均，以确定期货合约的理论价值。 还需考虑可交割债券的供应量和市场流动性，因为这些因素会影响到实际交割时的价格。

3. 利率期限结构模型

利率期限结构模型用于描述不同期限债券收益率之间的关系，并预测未来的利率走势。常用的模型包括：Nelson-Siegel模型、Svensson模型等。这些模型通过参数估计，来拟合现有的收益率曲线，并预测未来不同期限的收益率。在计算国债期货价格时，可以使用这些模型预测未来交割月份的收益率，从而计算出期货合约的理论价格。模型参数的选择和模型的拟合精度会直接影响到预测结果的准确性。 选择合适的模型需要考虑数据样本的特性和市场环境。例如，在市场波动较大的时期，可能需要使用更复杂的模型来捕捉市场变化。

4. 基差 (Basis)

基差是指国债期货价格与与其对应的现货价格之间的差价。基差的波动受到多种因素的影响，包括市场供求关系、交割成本、市场情绪等等。在计算国债期货价格时，基差是一个重要的考虑因素。 一个正基差表示期货价格高于现货价格，反之则为负基差。 基差的变化往往反映了市场对未来利率变化的预期以及市场流动性状况。 对于投资者来说，准确预测基差的变动至关重要，因为这直接关系到期货交易的盈亏。 通常情况下，投资者会参考历史基差数据以及市场信息来预测未来的基差，并将其融入到期货价格的计算中。

5. 市场风险溢价

市场风险溢价指的是投资者为了承担持有国债期货的风险而要求获得的额外收益。这种溢价会随着市场环境的变化而波动。在市场风险偏好较高时，风险溢价会降低；反之，在市场风险偏好较低时，风险溢价会升高。 计算国债期货价格时，需要考虑市场风险溢价的影响，这通常会体现在模型参数的设定中。 准确评估市场风险溢价具有一定的难度，因为其受到多种因素的影响，包括宏观经济形势、市场情绪、投资者预期等。 投资者通常会使用历史数据、市场指标以及定性分析方法来评估市场风险溢价，并以此来调整其期货价格的计算结果。

6. 资金成本

资金成本是持有国债期货合约期间需要支付的融资成本。这部分成本会影响到期货价格的计算，尤其是在持有期较长的情况下。资金成本的计算需要考虑多个因素，包括融资利率、保证金比例等。 在计算期货价格时，通常需要将资金成本的因素考虑其中，以获得更准确的理论价格。 不同的投资者可能有不同的资金成本，这会导致他们对期货价格的估值存在差异。 在实际交易中，投资者需要根据自身的资金成本情况来调整其交易策略。

计算国债期货价格是一个复杂的过程，需要综合考虑多种理论变量。准确预测国债期货价格需要对这些变量有深入的理解，并掌握相应的模型和计算方法。 仅对部分关键变量进行了阐述，实际应用中可能还需要考虑其他因素，例如税收、交易费用等。 投资者在进行国债期货交易时，应谨慎评估各种风险，并根据自身风险承受能力制定相应的投资策略。